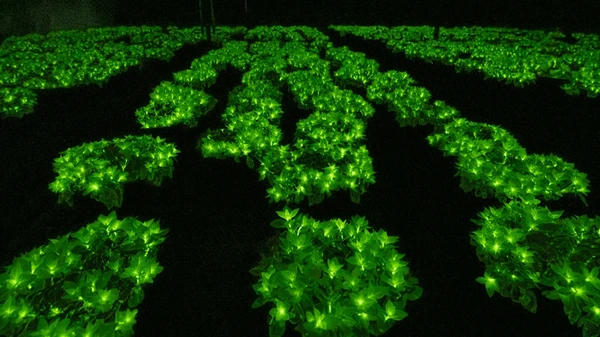
Diperkirakan terdapat 8 juta spesies tanaman di Bumi, masing-masing dengan karakteristik unik. Beberapa di antaranya bahkan memiliki kemampuan luar biasa: menyala dalam gelap. Bagaimana hal ini bisa terjadi?
Fenomena tanaman yang mampu ‘menyala’ di malam hari, baik pada daun maupun bunganya, menarik perhatian para peneliti. Sebagian besar disebabkan oleh kemampuan memantulkan cahaya. Namun, ada pula jenis tanaman yang mampu menghasilkan cahaya alami melalui rekayasa genetika.
5 Tanaman yang Mampu Menyala dalam Gelap
Berikut beberapa contoh tanaman yang dikenal karena kemampuannya ‘menyala’ dalam gelap, dengan beragam mekanisme yang berbeda.
1. Firefly Petunia
Firefly Petunia, dengan bunga yang unik, memancarkan cahaya alami berwarna hijau tanpa bantuan sumber cahaya eksternal.
Kemampuan bioluminesensi ini dihasilkan melalui rekayasa genetika. Para ilmuwan memasukkan gen dari jamur bioluminesensi *Neonothopanus nambi*, yang menghasilkan reaksi pemancar cahaya dengan molekul asam kafeat.
Gen jamur memungkinkan tanaman menghasilkan enzim yang mengubah asam kafeat menjadi luciferin (molekul pemancar cahaya), lalu mendaur ulangnya kembali menjadi asam kafeat, menciptakan siklus pemancaran cahaya.
2. Evening Primrose
Evening primrose, dengan warna kuningnya yang mencolok, tidak benar-benar ‘menyala’ dalam gelap. Namun, warna bunganya yang cerah membuatnya tampak bersinar di malam hari.
Keunikan evening primrose terletak pada ritme hariannya. Bunga ini menutup di siang hari dan mekar di malam hari pada waktu tertentu, menciptakan tampilan yang menonjol di antara kegelapan.
3. Glowing Moss
Glowing moss (*Schistostega pennata*) adalah lumut yang beradaptasi dengan lingkungan gelap. Ia mampu menyerap dan memantulkan cahaya dengan cara yang unik.
Sel-sel permukaan lumut memiliki lensa-lensa kecil yang memfokuskan cahaya redup ke dasar sel. Di sana, kloroplas bergerak untuk mengumpulkan cahaya. Cahaya hijau fluoresensi yang dihasilkan berasal dari pantulan cahaya yang difokuskan oleh kloroplas.
4. Moon Flower
Moon Flower (*Ipomoea alba*) tidak menghasilkan cahaya sendiri. Bunga putih ini tampak bersinar karena memantulkan cahaya, terutama cahaya bulan.
Keunikannya terletak pada waktu mekarnya. Moon Flower mekar di malam hari, sehingga pantulan cahaya putihnya semakin menonjol di kegelapan.
5. Dusty Miller
Dusty Miller, tanaman rendah asli Mediterania, memiliki daun-daun berbulu halus yang lebat.
Bulunya yang lebat membuat daun tampak keperakan dan bersinar, terutama saat terkena cahaya bulan di malam hari. Hal ini menciptakan efek ‘bercahaya’ pada tanaman.
Keberagaman mekanisme yang memungkinkan tanaman ‘menyala’ di gelap menunjukkan kekayaan dan kompleksitas alam. Mulai dari rekayasa genetika hingga adaptasi alami, tanaman-tanaman ini menawarkan keajaiban biologi yang menakjubkan.